Razón y proporción.
Para la resolución de problemas de proporcionalidad entre segmentos aplicamos el Teorema de Thales.
Razón es el valor de la relación entre las magnitudes de 2 segmentos. R= a/b.
Proporción es la igualdad entre dos razones: a/b = c/d (se expresa a es a b como c es a d)Razón es el valor de la relación entre las magnitudes de 2 segmentos. R= a/b.
Nomenclatura de los elementos:
términos: a, b, c y d
extremos: a y b
medios: c y d
Propiedad fundamental de la proporción: el producto de los extremos es igual al de los medios.
Cuarta proporcional.
Se conocen 3 de los 4 términos.
a/b = c/x
a/b = c/x
Tercera proporcional.
Se conocen 2 términos. Dos de ellos, sean los medios o los extremos, tienen el mismo valor.
a/b =b/x
a/b =b/x
Media proporcional.
Se desconocen los términos repetidos, medios o extremos.
a/x = x/b
a/x = x/b
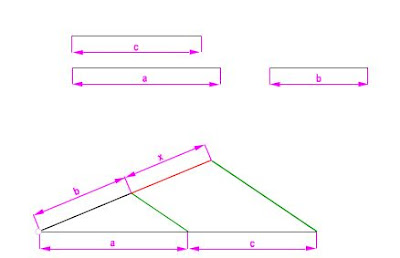
Se puede resolver el problema de 2 maneras diferentes, aplicando el teorema de la altura o el teorema del cateto.
Teorema de la altura. Suma de los segmentos dados.
La media proporcional es la altura de un triángulo rectángulo en el que se cumple el teorema que dice que, en un triángulo rectángulo, la altura sobre la hipotenusa es media proporcional entre los segmentos en que la divide.
Teorema del cateto. Diferencia de los segmentos dados.
Recomendable cuando los segmentos son de magnitudes grandes.
Y aplicación del teorema de Thales en este enlace.
La divina proporción.
Es la relación entre las partes y el todo.
Considerada la proporción ideal desde la época clásica. También llamada proporción áurea o número de oro. En el Renacimiento se conoce y difunde como Divina proporción.
En el Partenón las partes están relacionadas entre sí según la razón áurea.
Cuando el dato es a+b, el lado mayor del rectángulo, utilizamos la segunda opción.Considerada la proporción ideal desde la época clásica. También llamada proporción áurea o número de oro. En el Renacimiento se conoce y difunde como Divina proporción.
El valor del número de oro es de 1,618...
Los griegos fueron los primeros en utilizarlo. Lo obtuvieron al hallar la relación entre la diagonal de un pentágono y el lado, y le asignaron la letra fi.
Fi es un número irracional.
El llamado número de oro está relacionado con la naturaleza y con el arte, apareciendo repetidamente en el crecimiento de las plantas, en la distribución de las hojas, en la formación de las caracolas, en arquitectura, pintura, diseño...
Segmento áureo.
Es la división de un segmento en media y extrema razón. Es decir, la división de una longitud dada de manera que la parte menor sea a la mayor como la mayor a la total.
Dato: a
Dato: a+b
Dato: a
Dato: a+b
Rectángulo áureo.
Un rectángulo es áureo cuando el resultado de dividir el lado mayor y el menor es el número áureo, fi.
Cuando el dato es a, el lado menor del rectángulo, utilizamos la primera opción para su construcción.
Cuando el dato es a, el lado menor del rectángulo, utilizamos la primera opción para su construcción.
Observa la relación entre rectángulos áureos y la construcción de uno mayor.
Y ahora comprueba tu DNI, ¿se trata de un rectángulo áureo?
Y, para finalizar, dadle un vistazo a este vídeo. Os gustará.
Fuentes:
Departamneto de dibujo.
Matemáticas visuales.





















No hay comentarios:
Publicar un comentario